So if Assyria had its own number system, it was not important enough for anyone to write about. As it stands, most the information about Mesopotamian number systems is about Babylonian's system, with only a little knowledge about its predecessor, Akkadian, and Akkadian's predecessor, Sumerian.
 |
| A Sumerian List of Amounts of Grain |
The sumerians started by having a different mark for very quantity. For example, if you had three bushels of grain, you mark down three of the symbol for grain, and if you had four jars of oil, you would mark down three of the symbol for oil. This became inefficient for large quantities in which you would have to draw the same symbol thousands of times. Instead, they separated the symbols for quantities and products. The Sumerians would now draw a single symbol of the goods they were measuring next to the number measurements of the quantity of goods. The Sumerians had 60 different number signs. They used different systems for measuring distinct quantities, like sheep, and volumes, and had different symbols to express various quantities.
"In the basic sexagesimal system used for counting most discrete objects, a single object, a sheep or cow or fish, is denoted by a small cone. Ten cones equaled one small circle, six small circles equaled one big cone, ten big cones equaled was a big cone with a circle inside it, six of those was a large circle and ten large circles was given by a large circle with a small circle inside. This last unit was then worth 10x6x10x6x10 = 36000 base units. Note that the circle and "cone-shape" could be easily made by a stylus pressing on the clay, either vertically for the circle or at an angle for the cone." -Sumerian metrological numeration systems
.
The Akkadian's invented the abacus. They also were able to preform basic arithmetic. The Akkadian number system had a base of 60. The basics of the Babylonian system were taken from the Akkadian system, but the Babylonians expanded on it.
 |
| It probably didn't look much like this, but it gives the general idea |
So the Babylonian number system had the base of sixty. For hundreds of years, they did not have the numeral zero to hold the place of larger numbers, so 1 was the same as 60 and 3600. To differentiate between the different amounts, the Babylonians used a system similar to commas to mark place value. In this way, 74 was written as 1,14. Because the one is in the second place, it is actually sixty and so the in or number system would look like 1x60+14=74. 1,1,1 would be 3600+60+1=3661.
The numbers from 1 to 59 were expressed like this
The numbers are made up of combinations of the symbol
which represents 1 and the symbol
which represents 10. For 1, there is one wedge, for two there are two wedges and so on, but as they added for wedges, the patterns became a bit more complex. If the wedges touch each other, they become a single digit, so the number 2 would have two wedges touching and the number 60 would have a wedge a space in between and then another wedge. The Babylonians had difficulty expressing numbers with an empty space in the middle, like 301, because they had no zero to act as a placeholder.
 |
| Plimpton 322, a Babylonian table of numbers |
- Babylonians were able to express some fractions, but only those with a finite decimal on the base of 60. They also were only able to express fractions with one in the numerator. To express a fraction that had a different numerator, they had to write it ass the sum of two or more fractions that did have one in the numerator, so 3/4 would be written as 1/2+3/4.
- The Babylonians were also able to calculate the squares of numbers and compiled tables of the squares of numbers up to 59, meaning they figured out what the square of 59 was. They were also able tot compute some cubes of numbers.
- To ease multiplication, the Babylonians used the formulas ab = [(a + b)2 - a2 - b2]/2 and ab = [(a + b)2 - (a - b)2]/4. They were able to only use squares to multiply any numbers. That principle was all they needed for any multiplication procedure.
- They did not have long division and instead relied on the fact that a/b = a × (1/b) to conduct division operations. So when they divided numbers, they relied on reciprocal tables of fractions. (These would look different than our reciprocals because they worked with a base of 60.)
- Babylonians worked with Pythagorean triples. a^2+b^2=c^2 They did not have a way of expressing algebraic variables. They could also solve linear equations. They also worked with some geometry, as evidenced by their recognition that Pythagorean Triples related to right triangles.
- The Babylonians used their knowledge of mathematics to compile a 360 day calendar and twelve hour days. Each hour consisted of 60 minutes, but the minutes were twice as long as the minutes we have today.
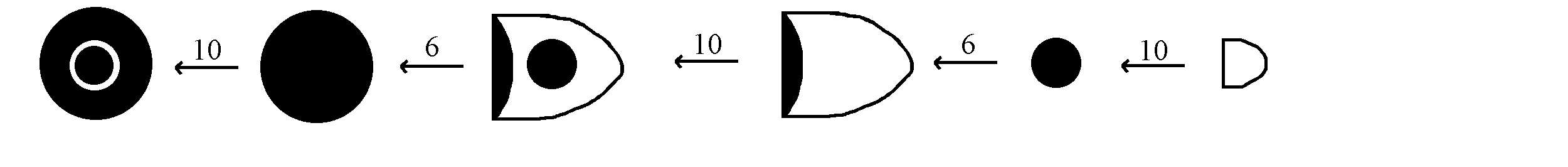

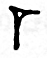
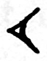
Wow, I've always taken advantage of our beautiful 10 digit system, but I've always thought that that would be the natural system. It seems that early Mesopotamian civilizations were able to utilize base 6 systems and fair okay with it, however is it more difficult? I wonder why not just go off ten since we have ten fingers and ten toes?
ReplyDeleteWow, cool! It makes sense! I think it get it! BUt I'm a little confused on something--did they base the numbers on 60 because they had 60 number signs to begin with?
ReplyDeleteThere is a lot of speculation as to why they chose 60, but the ideas are all pretty different, so I really have no idea. One historian thought that they might have used 6 as a base because they had a 360 day year, but that begs the question of which came first, the counting system or the calendar, astrology or mathematics? I don't know. Maybe they just got tired of making up new numbers when they got to fifty-nine and so decided to stick with it. You have to remember that it was the system they developed and it was the only thing they used. They didn't have other systems to compare it to. We are just so used to our standard way of counting that anything else seems illogical.
ReplyDeleteGoing off of what Catherine just pointed out, think about our system of time. We base our time off of 60 and really, is it that much more difficult than 10? I don't think so. It's all about what you're used to. The same goes for language in general. I've always thought that English was such an easy language to understand and learn, but in reality it's not. I discovered this a month or so ago when I was trying to help a guy in my ward work on learning English. It was so difficult to explain!
ReplyDeleteI think our brains have the capacity to learn all languages equally well. We just get used to a certain language or way of thinking and our brains become lazy in a sense. We become accustomed to one thing and pretty soon, everything besides that one thing seems difficult.
This is a fascinating post. I agree with Kacee- our system seems easier because it is familiar. Perhaps the nature of their transactions facilitated the use of a different number base. Maybe it was easier to have one system by which they could refer to either time or use to keep track of their transactions. It is kind of strange that we have a different kind of system for time.
ReplyDelete